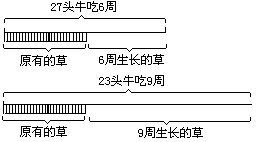
【例题】 牧场上有一片匀速生长的草地,可供27头牛吃6周,或供23头牛吃9周.那么它可供21头牛吃几周?
这类问题我们把它称为“牛吃草”问题。
解答这类问题,困难在于草的总量在变,它每周都在均匀地生长,时间愈长,草的总量越多。草的总量是由两部分组成的:①草场上原有的草量;②草场每周生长而新增的草量。(可参见下图)因此,必须设法找出这两个量来。
下面就用开头的题目为例进行分析。
我们不防假设每头牛每周吃草量为1。从上面的线段图可以看出23头牛9周的总草量比27头牛6周的总草量多,多出部分相当于3周新生长的草量。27头牛6周吃草量相当于27×6=162。23头牛9周吃草量相当于23×9=207。这样一来可以认为每周新生长的草量相当于(207-162)÷(9-6)=15。
需要解决的第二个问题是牧场上原有草量是多少?用27头牛6周的总吃草量减去6周新生长的草量(即15×6=90)即为牧场原有草量。
所以牧场上原有草量为27×6-15×6=72。
牧场上的草21头牛几周才能吃完呢?解决这个问题相当于把21头牛分成两部分.一部分看成专吃牧场上原有的草,另一部分看成专吃新生长的草。但是新生的草只能维持15头牛的吃草量,故分出15头牛吃新生长的草,另一部分21-15=6(头)牛去吃原有的草.所以牧场上的草够吃72÷6=12(周),也就是这个牧场上的草够21头牛吃12周。问题得解。
【练习题】一只船发现漏水时,已经进了一些水,水匀速进入船内.如果10人淘水,3小时淘完;如5人淘水8小时淘完.如果要求2小时淘完,要安排多少人淘水?
【解析】设每个人每小时的淘水量为“1”。
船内原有水量与3小时内漏水总量之和1×3×10=30
船内原有水量与8小时漏水量之和为1×5×8=40
每小时的漏水量等于8小时与3小时总水量之差÷时间差,
即(40-30)÷(8-3)=2(即每小时漏进水量为2个单位,相当于每小时2人的淘水量)。
船内原有的水量等于10人3小时淘出的总水量-3小时漏进水量。3小时漏进水量相当于3×2=6人1小时淘水量.所以船内原有水量为30-(2×3)=24。
如果这些水(24个单位)要2小时淘完,则需24÷2=12(人),但与此同时,每小时的漏进水量又要安排2人淘出,因此共需12+2=14(人)。
从以上这两个例题看出,不管从哪一个角度来分析问题,都必须求出原有的量及单位时间内增加的量,这两个量是不变的量。有了这两个量,问题就容易解决了。同时,我们也可以避免繁冗的方程计算。