行程问题是公务员考试数学运算部分的经典题型,主要研究物体速度、时间、路程之间的关系。
路程=速度×时间,时间=路程÷速度,速度=路程÷时间。
上述公式是行程问题的核心公式,简单的行程问题,比较容易从题干中找出速度、时间、路程三个量中的已知量后利用核心公式求解。
与基本的行程问题相比,相遇问题涉及两个或多个运动物体,解题过程则较为复杂。
在相遇问题中,有相遇路程=速度和×时间,时间=相遇路程÷速度和,速度和=相遇路程÷时间。
对较复杂的行程问题,必须弄清物体运动的具体情况:
如运动的方向(相向,同向),出发的时间(同时,不同时),出发的地点(同地,不同地),运动的路线(封闭,不封闭),运动的结果(相遇、追及、交错而过、相距多少)等。
多次相遇问题就属于比较复杂的一类问题。解决这类问题的关键是找出一共行驶了多少个全程,从而找出三量中的路程。在过程复杂时,可借助线段图分析。
按照路线的不同,多次相遇问题可分为直线多次相遇问题与环形路线多次相遇问题:
一、直线多次相遇问题
直线多次相遇问题的结论:从两地同时出发的直线多次相遇问题中,第n次相遇时,路程和等于第一次相遇时路程和的(2n-1)倍;每个人走的路程等于他第一次相遇时所走路程的(2n-1)倍。
例题1:甲、乙两车同时从A、B两地出发相向而行,两车在距B地64千米处第一次相遇。相遇后两车仍以原速继续行驶,并且在到达对方出发点后,立即沿原路返回。途中两车在距A地48千米处第二次相遇,问两次相遇点相距多少千米?
A.24 B.28 C.32 D.36
解析:此题答案为C。直线二次相遇问题,具体运动过程如下图所示。
由上图可知,第一次相遇时,两个车走的总路程为A、B之间的距离,即1个AB全程。第二次相遇时甲、乙两车共走了3个AB全程,即两车分别走了第一次相遇时各自所走路程的3倍。可知乙车共走了64×3=192千米,AB间的距离为192-48=144千米,故两次相遇点相距144-48-64=32千米。
例题2:甲、乙两人在长30米的泳池内游泳,甲每分钟游37.5米,乙每分钟游52.5米。两人同时分别从泳池的两端出发,触壁后原路返回,如是往返。如果不计转向的时间,则从出发开始计算的1分50秒内两人共相遇了多少次?
A.5 B.2 C.4 D.3
解析:此题答案为D。直线多次相遇问题,利用结论:从两地同时出发的直线多次相遇问题中,第n次相遇时,两人所走的路程和等于第一次相遇时所走路程和的(2n-1)倍,第一次相遇甲、乙的路程和为泳池长度,即30米。1分50秒时两人共游了(37.5+52.5)×=165米。165÷30=5……15,而5=2×3-1,因此两人共相遇了3次。
二、环形路线多次相遇问题
环形路线问题的难点在于寻找路程,找出路程,题目便迎刃而解。
如下图所示:
甲、乙在同一点出发,反向而行,当甲乙第一次相遇时,共跑了一圈。则甲路程+乙路程=跑道周长;
第二次相遇时,把他们第一次相遇的地点作为起点来看,第二次相遇时,他们又共同跑了一圈,即第二次相遇时甲乙总共跑了2圈;
……
归纳可知,每相遇一次,甲、乙就共同多跑一圈,因此相遇的次数就等于共同跑的圈数。得到公式甲总路程+乙总路程=跑道周长×n(n为相遇次数)
从而可得结论:
从同一点出发,反向行驶的环形路线问题中,初次相遇所走的路程和为一圈。如果最初从同一点出发,那么第n次相遇时,每个人所走的总路程等于第一次相遇时他所走路程的n倍。
例题1:老张和老王两个人在周长为400米的圆形池塘边散步。老张每分钟走9米,老王每分钟走16米。现在两个人从同一点反方向行走,那么出发后多少分钟他们第二次相遇?
A.16 B.32 C.25 D.20
解析:此题答案为B。环形多次相遇问题,每次相遇所走的路程和为一圈。因此第二次相遇时,两人走过的路程和刚好是池塘周长的2倍,相遇时间=路程÷速度和,即400×2÷(9+16)=32分钟。
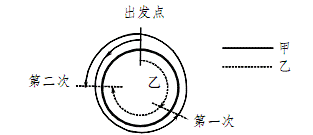
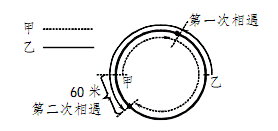
例题2:如图所示,甲和乙两人分别从一圆形场地的直径两端点同时开始以匀速按相反的方向绕此圆形路线运动,当乙走了100米以后,他们第一次相遇,在甲走完一周前60米处又第二次相遇,则这个圆形场地的周长为多少米?
A.320 B.360 C.420 D.480
解析:此题答案为D。观察图形,当甲、乙第一次相遇时,甲乙共走完圈的路程,当甲、乙第二次相遇时,甲乙共走完1+=圈的路程。所以从开始到第一、二次相遇所需的时间比为1∶3,即第二次相遇时乙行走的总路程为第一次相遇时行走的总路程的3倍,为100×3=300米。
甲、乙第二次相遇时,共行走(1圈-60)+300=圈,解得1圈=480米,即圆形场地的周长为480米。