一、基本原理
将三个苹果放到两只抽屉里,想一想,可能会有什么样的结果呢?要么在一只抽屉里放两个苹果,而另一只抽屉里放一个苹果;要么一只抽屉里放有三个苹果,而另一只抽屉里不放。这两种情况可用一句话概括:一定有一只抽屉里放入了两个或两个以上的苹果。虽然哪只抽屉里放入至少两个苹果我们无法断定,但这是无关紧要的,重要的是有这样一只抽屉放入了两个或两个以上的苹果。
如果我们将上面问题做一下变动,例如不是将三个苹果放入两只抽屉里,而是将八个苹果放到七只抽屉里,我们不难发现,这八个苹果无论以怎样的方式放入抽屉,仍然一定会有一只抽屉里至少有两个苹果。
在公务员考试数学运算中,考查抽屉原理问题时,题干通常有“至少……,才能保证……”这样的字眼。
我们下面讲述一下抽屉原理的两个重要结论:
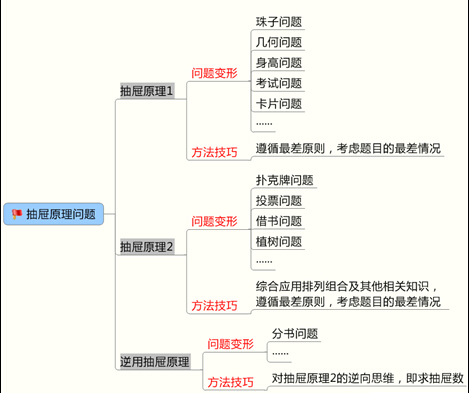
①抽屉原理1
将多于n件的物品任意放到n个抽屉中,那么至少有一个抽屉中的物品件数不少于2。(也可以理解为至少有2件物品在同一个抽屉)
②抽屉原理2
将多于m×n件的物品任意放到n个抽屉中,那么至少有一个抽屉中的物品的件数不少于m+1。(也可以理解为至少有m+1件物品在同一个抽屉)
公务员考试中,抽屉原理问题通常与其他问题相结合来进行考查,一般只有抽屉原理1、抽屉原理2和逆用抽屉原理三种类型。解抽屉原理问题的常用的方法是遵循最差原则,即考虑最差情况,其本质都是抽屉原理问题的基本原理。
二、题型精讲
(一)利用抽屉原理1
【例题】有20位运动员参加长跑,他们的参赛号码分别是1、2、3、…、20,至少要从中选出多少个参赛号码,才能保证至少有两个号码的差是13的倍数?
A.12 B.15 C.14 D.13
【解析】若想使两个号码的差是13,考虑将满足这个条件的两个数放在一组,这样的号码分别是{1、14}、{2、15}、{3、16}、{4、17}、{5、18}、{6、19}、{7、20},共7组。还剩下号码8、9、10、11、12、13,共6个。考虑最差的情况,先取出这6个号码,再从前7组中的每一组取1个号码,这样再任意取出1个号码就能保证至少有两个号码的差是13的倍数,共取出了6+7+1=14个号码。
(二)利用抽屉原理2
【例题】一个口袋中有50个编上号码的相同的小球,其中编号为1、2、3、4、5的各有10个。一次至少要取出多少小球,才能保证其中至少有4个号码相同的小球?
A.20个 B.25个 C.16个 D.30个
【解析】将1、2、3、4、5五种号码看成5个抽屉。要保证有一个抽屉中至少有4件物品,根据抽屉原理2,至少要取出5×3+1=16个小球,才能保证其中至少有4个号码相同的小球。
(三)利用最差原则
最差原则说的就是在抽屉问题中,考查最差的情况来求得答案。因为抽屉原理问题所求多为极端情况,故可以从最差的情况考虑。从各类公务员考试真题来看,“考虑最差情况”这一方法的使用广泛而且有效。
【例题】从一副完整的扑克牌中,至少抽出多少张牌,才能保证至少6张牌的花色相同?
A.21 B.22 C.23 D.24
【解析】一副完整的扑克牌包括大王、小王;红桃、方块、黑桃、梅花各13张,分别是A、2、3、4、5、6、7、8、9、10、J、Q、K。要求6张牌的花色相同,考虑最差情况,即红桃、方块、黑桃、梅花各抽出5张,再加上大王、小王,此时共取出了4×5+2=22张,此时若再取一张,则一定有一种花色的牌有6张。即至少取出23张牌,才能保证至少6张牌的花色相同。
【例题】一个布袋里有大小相同、颜色不同的一些小球,其中红的10个,白的9个,黄的8个,蓝的2个。一次至少取多少个球,才能保证有4个相同颜色的球?
A.12 B.13 C.14 D.15
【解析】从最坏的情况考虑,红、白、黄三种颜色的球各取了3个,蓝色的球取了2个,这时共取球3×3+2=11个,若再取1个球,那么不管取到何种颜色的球,都能保证有4个相同颜色的球,故至少要取12个。
(四)与排列组合问题结合
【例题】某区要从10位候选人中投票选举人大代表,现规定每位选举人必须从这10位中任选两位投票,问至少要有多少位选举人参加投票,才能保证有不少于10位选举人投了相同两位候选人的票?
A.382 B.406 C.451 D.516
【解析】从10位候选人中选2人共有C =45种不同的选法,每种不同的选法即是一个抽屉。要保证有不少于10位选举人投了相同两位候选人的票,由抽屉原理2知,至少要有45×9+1=406位选举人投票。
(五)与几何问题结合
【例题】在一个长4米、宽3米的长方形中,任意撒入5个豆,5个豆中距离最小的两个豆距离的最大值是多少米?
A.5 B.4 C.3 D.2.5
【解析】将长方形分成四个全等的小长方形(长为2米,宽为1.5米),若放5个豆的话,则必有2个豆放在同一个小长方形中,二者之间的距离不大于小长方形对角线长,因此5个豆中距离最小的两个豆距离的最大值是2.5米。